去年の冬、論理プログラミング言語「Prolog」を学習して、それ以来全く Prolog には触れていませんでした。このまま忘れてしまうのも勿体ないなと思い、復習も兼ねてメモしておきます。
なお、この記事は初学者が初学者なりの理解・解釈で書いているので、必ずしも正しい情報であることは保証できません。その点ご了承ください。

論理プログラミングとは

命題論理に基づいた言語で、Haskell のような関数型言語と同じく非手続き型言語なのでプログラムの順序は関係ありません。
論理プログラミング言語に特徴的なのは、ただ単にプログラムを書いて動かす、というわけではなく、ルールを定義し、その上で質問（= 命題）を入力するという点です。プログラマは複数のルールを定義し、インタプリタに対して質問を投げかけると、ルールに基づいた回答を返したり、真が成立する値を返してくれます。

日本語で例えるなら、

すべての人間は死ぬ。
ソクラテスは人間である。

と定義したときに、

ソクラテスは死ぬ？

という質問を投げかけたら、正（true）が解答として導かれます。
あるいは、

何が人間に当てはまるか？

という質問を投げかけたら、「ソクラテス」という解答が得られます。

論理プログラミングには2種類の質問が定義されています。

• 1つ目の「ソクラテスは死ぬ？」という質問に対しては、true or false で解答が導かれます。Prolog では、これは「融合 (resolution)」といいます。
• 2つ目の「何が人間に当てはまるか？」という質問に対しては、単語や数値などで解答が得られます。Prolog では、これは「単一化 (unification)」といいます。

命題論理

命題論理の基礎的な部分をさらっとまとめておきます。ここは読み飛ばしていただいて構いません。

含意と等価

• 含意（=>）：a ならば b
• 等価（<=>）：a = b

真を true、偽を false とし、a と b のすべての組み合わせに対する含意と等価の結果を表に表すとこうなります。

a	b	含意 (a=>b)	等価 (a<=>b)
false	false	true	true
false	true	true	false
true	true	false	false
true	true	true	true

等価は直感の通りで、a と b の値が同じなら true、そうでなければ false です。
含意は「a という仮定が成り立つなら b も成り立つ」という意味です。「a が成り立たないなら b も成り立たない」と「a が成り立つなら b が成り立つ」は真、「a が成り立たないなら b が成り立つ」「a が成り立つなら b は成り立たない」は偽と定義されています。

一階述語論理

命題論理に加え、個体変項 (Predicate) が加わったものが一階述語論理です。個体変項とは、True or False 以外の解を有するもので、値や文字列などがこれに該当します。

量化子

• 全称量化子 ∀x : どれか一つが存在するなら True （すべての…）
• 存在量化子 ∃x : 一つ以上存在するなら True （とある…）

例1）Mother (x) => ∃y, Child(y) ∧ Has_Child(x, y)

「x が母親なら => y が存在して、y は x の子供である」

例2）∀x, HasWheels(x) ∧ HasTrailer(x) => Truck(x)

「ある x にホイールとトレーラーがあれば => x はトラックである」

Prolog を使ってみる

環境にインストールすることもできますが、SWISH というブラウザで利用できるオンライン環境がお手軽でおすすめです。
https://swish.swi-prolog.org

Prolog の基礎

ルールの定義

基本的な構文は次のとおりです。

頭部 :- 本体部.

これが頭部 = 本体部という論理関係を表す構文になります。
構文で特徴的なのは、必ず最後にピリオド(.) を打つ必要があることです。

事実

ルール上で True となる規則を定義するのが事実 (fact) です。
例）bob は人間である

human(bob).

これは次のように書くことも可能です。

human(bob) :- true.

規則

「○○ ならば △△ である」といったルールを定義するのが規則です。

例）人間は動物である

human(X) :- animal(X).

複数の条件（副目標）の指定にはカンマ(,) で区切って書き連ねます。

頭部 :- 副目標1, 副目標2, ...

質問 (query)

ルールを定義したら、今度はインタプリタに対して質問をしてみます。 質問には「融合 (resolution)」と「単一化 (unification)」の2つがあります。
以降、?- から始まるコードブロックはすべてインタプリタに対する質問入力です。

融合 (resolution)

その質問が成立するか否かを true or false で回答する質問が「融合」です。
例）

?- human(bob).
true

ルールにはhuman(bob).が定義されていますので、質問に対する回答は true になります。
例えば、定義していないものを質問した場合

?- human(alice).
false

alice はルールに存在しないので、false が返されます。
alice を true にするには、両方をルールに定義する必要があります。
ルール：

human(bob).
human(alice).

質問：

?- human(alice).
true

このように、Prolog では true となるすべての条件を定義し、定義されていないものに関しては解は false になります。

単一化 (unification)

もう一つの質問の種類として、「単一化」があります。これは、解 true が成立する条件を回答とする質問になります。単一化の質問を行う場合、X などといった変数を質問に置きます。
例）

?- human(X).
X = bob
X = alice

束縛変数

変数間の関係もルールに定義可能です。

例）X = X なら true
ルール：

p(X, X).

質問：

?- p(1, 1)
true
?- p(1, 2)
false
?- p(A, B)
A = B

例

例1) トラックの定義

ルール：

haswheels(v1).
haswheels(v2).
haswheels(v3).
hastrailer(v1).
hastrailer(v2).
truck(X) :- haswheels(X), hastrailer(X).

質問：

?- truck(T).
T = v1
T = v2
false

v1, v2 は truck(X) の条件に合致するので、単一化の解になります。一方、v3 は条件に当てはまらないので false となります。

例2) 家族関係の定義

ルール：

parent_child(X, Y) :- father_child(X, Y).
parent_child(X, Y) :- mother_child(X, Y).
brother(X, Y) :- parent_child(Z, X), parent_child(Z, Y).

father_child(hiroshi, shinnosuke).
father_child(hiroshi, himawari).
mother_child(misae, shinnosuke).

質問：

?- brother(X, Y).
X = Y, Y = shinnosuke
X = shinnosuke,
Y = himawari
X = himawari,
Y = shinnosuke
X = Y, Y = himawari
X = Y, Y = shinnosuke

X != Y を定義していないので X = Y などが単一化の解として現れてしまいますが、これによって兄弟関係が導出可能です。

発展

再帰処理

再帰を使って、n 階層に渡る関係を定義することも可能です。例えば

ancestry(X, Y) :- parent(X, Y).
ancestry(X, Y) :- parent(X, Z), ancestry(Z, Y).

parent(ginnosuke, hiroshi).
parent(tsuru, hiroshi).
parent(yoshiharu, misae).
parent(hisae, misae).
parent(hiroshi, shinnosuke).
parent(misae, shinnosuke).
parent(hiroshi, himawari).
parent(misae, himawari).

とすれば、

?- ancestry(ginnosuke, shinnosuke).
true

このようにして何世代でも家族関係を定義することができます。

再帰処理の定義でミソとなるのは、停止条件（base fact）が必要となる点です。C言語などで再帰処理を実装するときも何らかの条件があってループから抜けなければ無限ループに陥ってしまうのと同じように、Prolog での再帰処理もループから抜けるための条件がなければ無限ループに陥ります。
ここでは、ancestry(X, Y) :- parent(X, Y). を停止条件として定義しています。つまり、再帰処理の中で「いつか X と Y が親子という関係が導き出せたら正」と定義し、それが成立するか否かで判断します。

グラフの定義

グラフも命題論理で定義できます。Prolog では2つのノード間の関係を定義すれば OK です。
例えば、こんなグラフを定義してみます。

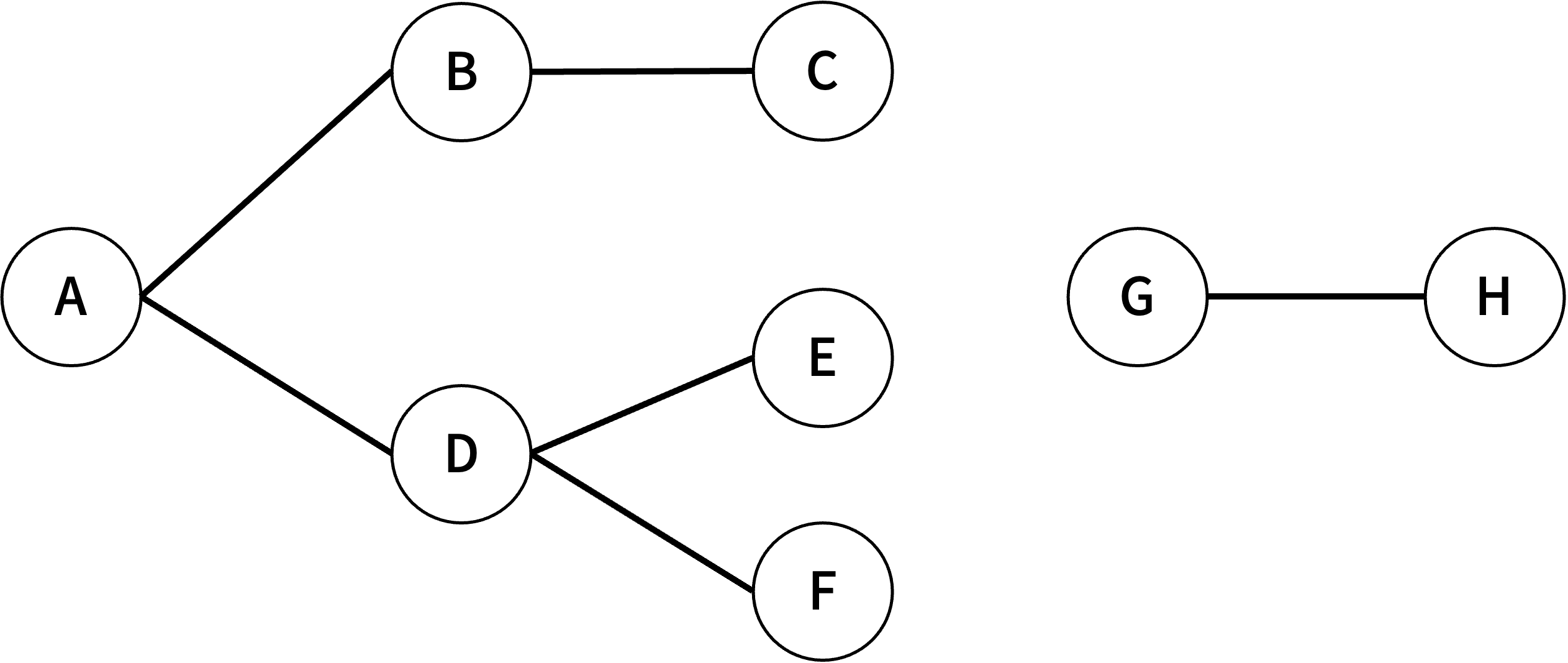
Prolog での定義は次のとおりです。

edge(a, b).
edge(b, c).
edge(a, d).
edge(d, e).
edge(d, f).
edge(g, h).

まずは定義を確認してみます。

?- edge(a, b).
true
?- edge(a, f).
false
?- edge(X, Y).
X = a,
Y = b
X = b,
Y = c
X = a,
Y = d
X = d,
Y = e
X = d,
Y = f
X = g,
Y = h

次に、ノードからノードまでたどり着けるか？を定義してみます。定義は以下のとおりです。

link(X, Y) :- edge(X, Y).
link(X, Y) :- edge(X, Z), link(Z, Y).

ここで、link(X, Y) :- link(X, Z), edge(Z, Y). としてしまうと無限ループになってしまうので要注意です。
質問：

?- link(a, b).
true
?- link(a, f).
true
?- link(a, h).
false

無事、グラフを定義することができました。

リストの定義

前後の要素の関係を定義することでリストが定義できます。[X|Xs] で「X がリスト Xs の末尾である」状態を定義します。

list([]).
list([_|Xs]) :- list(Xs).

質問：

?- list([1,2,3])
True

これを用いて、まずは要素がリストに含まれているか探索する命題を定義してみます。

member(X, [X|Xs]).
member(X, [Y|Ys]) :- member(X,Ys).

1行目は「X が Xs の先頭要素であること」を示す停止条件であり、2行目では再帰処理によってリストを探索します。

こうすることで、以下の質問が成立します。

?- member(1,[2,1]).
True.
?- member(X,[2,1,0)
X=2, X=1, X=0

おわりに

力尽きたのでこのへんで。気が向いたら続きを書きます。