先日、大学の講義で扱われた「秘密分散法」という手法の仕組みがとても興味深かったので、実際にPythonで実装してみました。

秘密分散法とは

一言で言えば暗号化の手法の一つ。暗号化したい1つの平文を複数の「シェア（分散片とも言う）」と呼ばれるデータに分散して保管することで、頑強性と秘匿性が確保されます。
平文をn個のシェアに分散し、k個（k≦n）以上のシェアが揃えば復元できるようにします。つまり、分割したシェアのうち、全てが集まらなくても、k個集まればk個のシェアから1つの平文に復元できるというわけです。よってn-k個のシェアを紛失しても復元できるので、頑強性が確保されます。また、シェアがk個未満しか集まらなかった場合、復元はできないので秘匿性が確保されます。

(k,n)閾値法

秘密分散法のアルゴリズムの1つ。1979年にRSA暗号の提唱者の1人であるShamir博士によって提唱された手法です。

(k,n)閾値法のアルゴリズム

例として、(2,3)閾値法で考えてみます。つまり、k=2、n=3なので、合計3個のシェアがあって2個以上のシェアで復元できます。また、平文は仮にS=123とします。

1. 有限体を作る

まずは要素数p（ただし、p>nかつp>Sでpは素数）の有限体Fpを作ります。

\[F_p=\{0,1,...,p-2,p-1\}\]

n=3、S=123より大きい素数ということで、ここでは仮にp=127とします。

\[F_p=\{0,1,2,..., 125, 126\}\]

2. シェアを生成する

n=3個のシェアを生成します。i番目のシェアWiは次の数式で表されます。

\[W_i=f(α_i)=S+A_1α_i+A_2α_i^2+…+A_{k-1}α_i^{k-1}\quad\quad(i=1, 2, ..., n)\]

ここで、A1，A2…は有限体Fpの中からランダムに選びます。

上記のシェアをn個分生成します。このとき、αiは0以外のFpの相異なる元とします。つまり、今回のようにp=127の場合、

\[α_i ∈ \{1, 2, ..., 125, 126\}\]

であり、αiは1〜126のいずれかの値を取ります。さらに、αiは他のシェアのものと同じ値をとってはいけないというわけです。

今回はAとαを以下のように設定。

\[A_1 = 3\] \[α_1 = 1, α_2 = 2, α_3 = 3\]

そして次のようにn=3個のシェアW1〜W3を生成しました。

\[W_1=F(α_1)=S+A_1α_1=123+3×1=126\] \[W_2=F(α_2)=S+A_1α_2=123+3×2=129\] \[W_3=F(α_3)=S+A_1α_3=123+3×3=132\]

3. 復元する

復元には先程生成したシェアのうち、k個以上のシェアが必要です。復元する上ではラグランジュ補間を用います。

\[f(t)=\sum_{j=1}^kf(α_{i_j})\frac{(t-α_{i_1})…(t-α_{i_{j-1}})(t-α_{i_{j+1}})…(t-α_{i_k})}{(α_{i_j}-α_{i_1})…(α_{i_j}-α_{i_{j-1}})(α_{i_j}-α_{i_{j+1}})…(α_{i_j}-α_{i_k})}\]

ここで、t=0（つまり、切片を求める）とすることで復元できます。なお、コンピュータで扱える数は有限ですので、多くの場合は有限体上で計算されます。

\[f(t)=\sum_{j=1}^kf(α_{i_j})\frac{(t-α_{i_1})…(t-α_{i_{j-1}})(t-α_{i_{j+1}})…(t-α_{i_k})}{(α_{i_j}-α_{i_1})…(α_{i_j}-α_{i_{j-1}})(α_{i_j}-α_{i_{j+1}})…(α_{i_j}-α_{i_k})}\bmod p\]

実際に復元してみます。

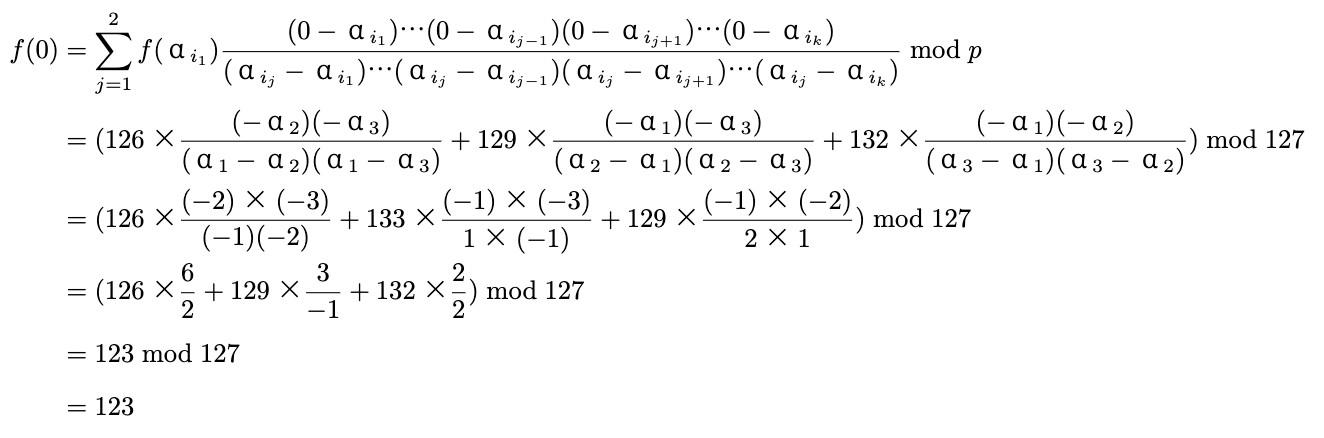
平文である「123」が復元できました。

なぜ復元できるのか？

グラフで表してみれば簡単です。(k,n)=(2,3)で考えてみます。例えば次の1次直線。

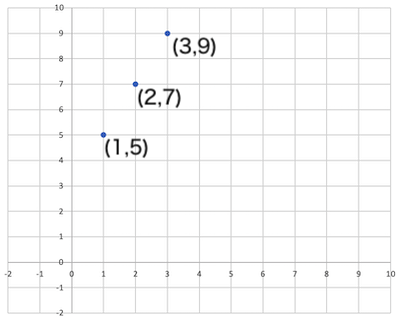
3つの点(1, 5)、(2, 7)、(3, 9)が与えられていれば簡単に1次式を導けます。答えはf(x)=2x+3で、この1次式より切片はf(0)=3です。この切片こそが、復元後の値、つまり平文に相当します。

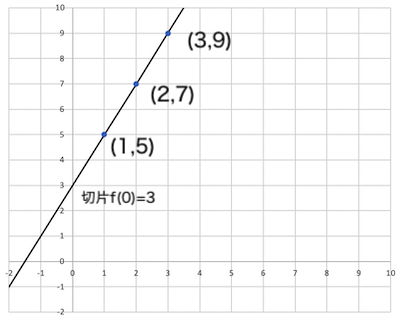
k=2ですから、2つの点(1, 5)と(2, 7)、(1, 5)と(3, 9)、あるいは(2, 7)と(3, 9)でも1次式と切片を導けます。

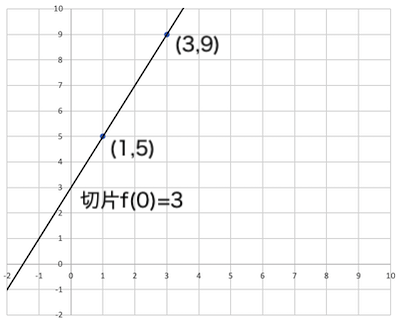
では、もし1つの点(1, 5)しか与えられていなかったら？

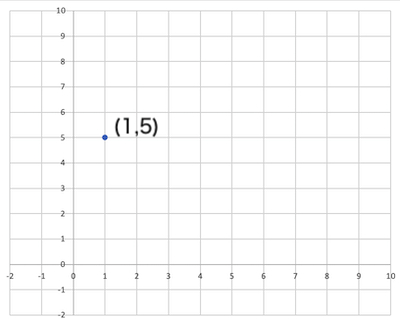
直線の引き方は無数にありますので、1点だけでは1次式も切片もわかりません。つまり、1<kであるので元の平文に復元できません。

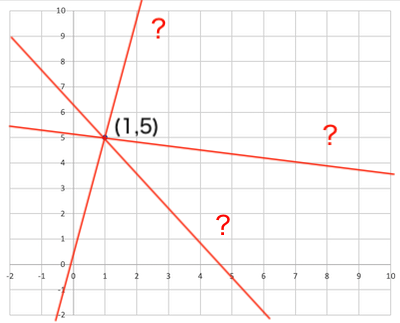
よって、k=2個以上のシェアが得られないと復元できないというわけです。

ラグランジュ補間は与えられた座標を通る式を導くための手法です。k個以上の座標を与えてやるとf(x)=2x+3が導けます。

Pythonで実装してみる

ここからが本題です。上記のアルゴリズムをPythonで実装してみます。

定義どおりに実装

初期値を上記の定義の通りにして実装します。下記のプログラムではシェアの生成と、シェアからの復元を同時に行います。なお、復元に用いるシェアの数はnums=k=2個としています。

# 初期値
n = 3      # シェアの個数
k = 2      # 復元に必要なシェアの個数
S = 123    # 平文
p = 127    # 有限体の個数（素数）

print("シェアの個数n =", n, "復元に必要なシェアの個数k =", k)
print("平文S =", S, "有限体の要素数p =", p)

# 有限体を生成する
# Fp = [0, 1, 2, ..., p-2, p-1]
Fp = range(0, p)
print("有限体Fp =", Fp)

# 係数A
A = [3]
print("A =", A)

# αを設定
alpha = [1, 2, 3]
print("alpha =", alpha)

# シェアを生成する
W = []
for i in range(n):
    w_i = S
    for j in range(k - 1):
        w_i += A[j] * pow(alpha[i], j + 1)
    W.append(w_i)

print("Shares: ", str(W))

# 復元する
Y = 0  # 復号した文
nums = k  # 復号に用いるシェアの数（k以上n以下）
for i in range(nums):
    # 分子部の計算
    numerator = 1
    for j in range(nums):
        if j == i:
            continue
        numerator *= -alpha[j]

    # 分母部の計算
    demominator = 1
    for j in range(nums):
        if j == i:
            continue
        demominator *= alpha[i] - alpha[j]

    # Yに加算
    Y = (Y + W[i] * (numerator / demominator)) % p

# 復元結果
print("復元後：Y =", Y)

シェアの個数n = 3 復元に必要なシェアの個数k = 2
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [3]
alpha = [1, 2, 3]
Shares:  [126, 129, 132]
復元後：Y = 123.0

Sharesに表示されている126、129、132が生成されたシェアです。今回はシェアのうち2つ、126と129を用いて復元しています。除算を伴うので実数に変換されていますが、元の平分である123が復元されました。うまい具合に動いているようです。

係数をランダムに選んでみる

係数に相当する配列Aとαを有限体Fpの中からランダムに選ばせてみます。

import random

# 初期値
n = 3      # シェアの個数
k = 2      # 復元に必要なシェアの個数
S = 123    # 平文
p = 127    # 有限体の個数（素数）

print("シェアの個数n =", n, "復元に必要なシェアの個数k =", k)
print("平文S =", S, "有限体の要素数p =", p)

# 有限体を生成する
# Fp = [0, 1, 2, ..., p-2, p-1]
Fp = range(0, p)
print("有限体Fp =", Fp)

# 係数Aをランダムに選ぶ
A = random.sample(Fp, k - 1)
print("A =", A)

# αをランダムに選ぶ
alpha = random.sample(Fp[1:], n)
print("alpha =", alpha)

# シェアを生成する
W = []
for i in range(n):
    w_i = S
    for j in range(k - 1):
        w_i += A[j] * pow(alpha[i], j + 1)
    W.append(w_i)

print("Shares: ", str(W))

# 復元する
Y = 0  # 復号した文
nums = k  # 復号に用いるシェアの数（k以上n以下）
for i in range(nums):
    # 分子部の計算
    numerator = 1
    for j in range(nums):
        if j == i:
            continue
        numerator *= -alpha[j]

    # 分母部の計算
    demominator = 1
    for j in range(nums):
        if j == i:
            continue
        demominator *= alpha[i] - alpha[j]

    # Yに加算
    Y = (Y + W[i] * (numerator / demominator)) % p

# 復元結果
print("復元後：Y =", Y)

今回は乱数を含むので、動作確認のため何度か実行してみました。

シェアの個数n = 3 復元に必要なシェアの個数k = 2
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [94]
alpha = [19, 39, 37]
Shares:  [1909, 3789, 3601]
復元後：Y = 123.0

シェアの個数n = 3 復元に必要なシェアの個数k = 2
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [106]
alpha = [65, 108, 93]
Shares:  [7013, 11571, 9981]
復元後：Y = 123.0

シェアの個数n = 3 復元に必要なシェアの個数k = 2
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [125]
alpha = [104, 119, 72]
Shares:  [13123, 14998, 9123]
復元後：Y = 123.0

シェアの個数n = 3 復元に必要なシェアの個数k = 2
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [16]
alpha = [101, 29, 25]
Shares:  [1739, 587, 523]
復元後：Y = 123.0

いずれもk = 2個のシェアで正しく復元できています。

ここで問題が…

では、nとkを大きくしてみたらどうか？と試してみたら、なんと復元後の値に誤差が出始めてしまった。

# 初期値
n = 11      # シェアの個数
k = 7       # 復元に必要なシェアの個数
S = 123     # 平文
p = 127     # 有限体の個数（素数）

シェアの個数n = 11 復元に必要なシェアの個数k = 7
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [68, 18, 103, 54, 23, 57]
alpha = [64, 31, 8, 52, 96, 13, 4, 24, 62, 73, 45]
Shares:  [3942639284603, 51299138426, 15971611, 1136078805803, 44809407504891, 285440486, 278123, 11095361883, 3259507026883, 8675305219886, 477789646758]
復元後：Y = 122.99998345389031

シェアの個数n = 11 復元に必要なシェアの個数k = 7
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [59, 87, 44, 19, 45, 113]
alpha = [8, 51, 75, 121, 70, 104, 87, 4, 118, 79, 96]
Shares:  [31203347, 2004041262690, 20218979603298, 355813742724970, 13370440212553, 143530816068659, 49225168271682, 518359, 306082867471897, 27608112304834, 88820201443995]
復元後：Y = 124.0

さらに大きくしてみると…

# 初期値
n = 97      # シェアの個数
k = 17      # 復元に必要なシェアの個数
S = 123     # 平文
p = 127     # 有限体の個数（素数）

シェアの個数n = 97 復元に必要なシェアの個数k = 17
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [30, 95, 62, 61, 91, 37, 38, 21, 10, 49, 12, 7, 120, 25, 103, 59]
alpha = [18, 98, 19, 125, 94, 119, 97, 35, 60, 33, 81, 73, 71, 15, 70, 115, 2, 48, 55, 112, 102, 14, 24, 53, 95, 107, 59, 32, 90, 120, 56, 61, 52, 110, 122, 103, 40, 31, 58, 68, 57, 8, 4, 124, 39, 44, 7, 41, 108, 101, 20, 86, 92, 34, 43, 22, 28, 72, 79, 75, 106, 42, 123, 114, 64, 3, 121, 38, 21, 6, 93, 27, 54, 51, 36, 84, 13, 85, 87, 46, 67, 105, 62, 109, 50, 11, 78, 89, 1, 88, 29, 116, 111, 99, 9, 45, 76]
Shares:  [7871714454402870314163, 4346676813415358879335031763306323, 18606738204856056302251, 212543445844481774944449355835472623, 2233113873766979274020326820878651, 96814778348047569571128761904817451, 3689492718251735945449123054469167, 314226390188722217273538923, 1713095497755992857767117895923, 122926863764472494409815343, 206967494291037515482681224717423, 39293203281397746506133449123023, 25210007936248103013029594912363, 433603570977672469323, 20098239795483961230215883043723, 56049923299592606991461093478017323, 8760467, 48563663661359815689650109723, 426864364960572730976323092523, 36734373978067088503645860302707867, 8238405500885211150092275561867467, 144896266584221579291, 767509561452212290796811, 236270627223389540667177392783, 2644594424455367330195067817955723, 17702619932934716047617645193769867, 1309796119247681842403584979531, 75251803906584808432631867, 1114548942264842951995027031080323, 110671974221596413595981287176667723, 569186150236295314344713848523, 2230672446134230188972052984303, 174308401811559731414284046467, 27541588005120023879637397415784923, 144142641860178900595549358789641667, 9628634414581533085352188950939883, 2645377854779044492550681323, 45356745731166529782442123, 996865407432730653633871416643, 12648676075532038119833052097763, 755111316586208754582232100367, 20407574327584043, 378986467171, 186931679292696473090628386741009011, 1766174576346395615500250091, 12108613955370529466123996051, 2478459017365867, 3923017358670349181132111183, 20540561966242156288096087451604243, 7038094841152684954538242994846543, 42092166037068909494723, 538989967255842553356629227068203, 1583592801780605557199574244908467, 197894229669061861788971731, 8389519383268305327700045963, 191958556339972751466667, 8951718619487685814930483, 31521980684201224525015770986667, 138806154897562181439753292266571, 60514491255246696475955941146123, 15235511268984752002481377470236323, 5762871923763309299797714467, 164235466111525292158677589714722123, 48746609734876084400148079662277491, 4802489284489112850956881360891, 4337800683, 126372319567754460060080395215547663, 1166901054393297861501245003, 91519842742208723202063, 218423628435723, 1882253004374188828585325374782063, 5013737259199303551883467, 318446762121069790236696801771, 127840093230140365447633011243, 492505647509175842598650403, 370067528662263789734934126827331, 44666697818053254703, 447106037660252272697806175665423, 648356063543505197961832535133867, 24617664833183344351632175963, 9983039805990816683047543391467, 13093607297406591135046505378899023, 2892203471222461944907750799867, 23800852633020337743358350067827631, 93186891420821163106951739123, 3154953787272629003, 113242663067617070848023224125083, 932293123496032658192678829474191, 943, 778270589364744444884243512510603, 15662021263286066702639471, 64369653003714884872270758250042883, 31828213510910612772240151034214603, 5112414583009862721380419092527211, 131414450876116431, 17333201407128780792892994223, 74776603747404074023467373122643]
復元後：Y = 103.66784533113241

シェアの個数n = 97 復元に必要なシェアの個数k = 17
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [79, 10, 26, 41, 126, 44, 57, 21, 18, 40, 43, 51, 102, 118, 83, 38]
alpha = [27, 51, 34, 96, 83, 99, 43, 12, 75, 40, 108, 92, 9, 26, 119, 42, 1, 125, 73, 4, 79, 116, 95, 90, 31, 105, 118, 57, 81, 70, 89, 11, 87, 107, 35, 24, 91, 76, 112, 69, 94, 22, 59, 123, 44, 23, 46, 65, 72, 114, 8, 33, 45, 39, 55, 93, 110, 61, 29, 84, 54, 115, 106, 80, 78, 53, 47, 100, 77, 104, 68, 67, 58, 16, 126, 36, 20, 38, 21, 5, 7, 32, 101, 111, 117, 50, 13, 10, 82, 37, 109, 56, 30, 48, 60, 15, 113]
Shares:  [3289665495153457650292224, 83104467374845137076535507520, 129303260797662246643495617, 2023196628948886991775607070688795, 197927793198468176057803948061760, 3307958489963514439690254950540352, 5463925631956943668483449600, 8467289565756561999, 39216300279424251105598407906048, 1724445007391899349713043283, 13285365839224735705591933948554735, 1025029085813224340340654837491199, 90478363908992892, 1804215040646944179731145, 62593356998078619997238130592990032, 3754319907333014016433195449, 1020, 137389138054954954770736734914228748, 25468403195117712688780735959420, 291935103447, 89923680620586909209951452129872, 41620950018151911573608227048424295, 1711515233349929903091112865362128, 721509189121915579707438560452233, 29681546642441588384256720, 8469830119981751398499111365420668, 54696168431140306930482727817712525, 490363323453632310960323964924, 134060869469931143239212447044220, 13030663795345763631316927582653, 603560913507516347215571764009212, 2141306543779019520, 419793654778422095655967056300624, 11450289228918919201834565324999424, 205221910772102571046989888, 504906543882601841699427, 860810068856705684578855026193920, 48454713978057555360565498298895, 23755613329745412182385021389663499, 10355750404854602018494313344332, 1445292329446825157120780691211557, 126556485858581354503149, 850319372592994065548322734592, 106169070888040727685295604625093120, 7883944821823983976593794607, 256590447042628276080720, 16020474715320741006898377045, 3990837167627182035303132416508, 20433275311979985057335332078899, 31521440836668026732150542080557937, 14195316493502835, 80358398684347321947192060, 11282750866564316852799484428, 1151704549545487512613570512, 277290787393839046788114757968, 1218278222235541499416858115340300, 17812125368718694537058459534145813, 1447752888538531289573188843020, 10261765707765113244380172, 239656254195172956036558824178567, 206897730717418250741954024397, 36242747800775221783471652343494208, 9854940457814351108714702648532345, 109933255275245510329783145542443, 73368471261796142334728824544565, 153534122375681102444109899340, 22577247828216561152807091024, 3884190251434018215745264126108023, 59704448481991905804535928051724, 7268867488998905943074045854915347, 8202435165079227726564509575575, 6474515082782035955813044405824, 647258916008927674430513263785, 805646079953394642795, 156048777825276386682721696828176645, 321520535497685017493651895, 27825329161829785973703, 761194386255578825883107805, 60414692297676482937420, 9191015720268, 1747615100105424, 49217965830946465844638299, 4553527320081097404462121939699020, 20583645498942624861519587527901520, 47740577152646277487890117933045324, 60589636688512584320884529073, 30031034934941549580, 475875720727037913, 163087026406348243581032171804049, 497590103849822458991906124, 15393463045843951114321336565921292, 369682834567884161961166358595, 17606806393872053861723493, 31589221450508764715000613195, 1111985250197615154636498616863, 289595000411559113808, 27381522633623026179848130161689980]
復元後：Y = 14.069935309092216

これはひどい。誤差が大きい上にブレまくりではないですか…

kを小さくした場合はnやpが大きくても誤差は小さく済みました。

# 初期値
n = 97      # シェアの個数
k = 3       # 復元に必要なシェアの個数
S = 123     # 平文
p = 127     # 有限体の個数（素数）

シェアの個数n = 97 復元に必要なシェアの個数k = 3
平文S = 123 有限体の要素数p = 127
有限体Fp = range(0, 127)
A = [78, 50]
alpha = [11, 26, 5, 24, 48, 15, 3, 13, 20, 57, 72, 104, 98, 46, 27, 115, 31, 110, 2, 69, 59, 45, 4, 112, 44, 111, 86, 121, 52, 118, 108, 89, 61, 40, 102, 82, 12, 68, 41, 42, 88, 23, 109, 30, 60, 9, 117, 47, 126, 105, 37, 8, 63, 28, 21, 116, 74, 114, 97, 107, 50, 49, 83, 25, 51, 113, 70, 75, 29, 122, 79, 56, 64, 125, 119, 71, 87, 53, 93, 95, 120, 32, 103, 18, 7, 94, 55, 66, 39, 92, 22, 58, 73, 81, 90, 96, 14]
Shares:  [7031, 35951, 1763, 30795, 119067, 12543, 807, 9587, 21683, 167019, 264939, 549035, 487967, 109511, 38679, 670343, 50591, 613703, 479, 243555, 178775, 104883, 1235, 636059, 100355, 624831, 376631, 741611, 139379, 705527, 591747, 403115, 190931, 83243, 528279, 342719, 8259, 236627, 87371, 91599, 394187, 28367, 602675, 47463, 184803, 4875, 693699, 114239, 803751, 559563, 71459, 3947, 203487, 41507, 23811, 681971, 279695, 658815, 478139, 580919, 129023, 123995, 351047, 33323, 134151, 647387, 250583, 287223, 44435, 753839, 318335, 161291, 209915, 791123, 717455, 257711, 385359, 144707, 439827, 458783, 729483, 53819, 538607, 17727, 3119, 449255, 155663, 223071, 79215, 430499, 26039, 172847, 272267, 334491, 412143, 468411, 11015]
復元後：Y = 122.99999999999955

誤差の原因

実行結果のSharesの部分を見ると分かる通り、kを大きくすると各シェアの値が肥大化しています。これはシェアの生成の際に1〜(k-1)乗した値の加算が行われる為です。
累乗によって増大化した数値同士の除算を伴うので、計算上の丸め誤差が原因かと思われます。実装する上で特に何も工夫しなかったからかな…
kが少ないほどシェアの数値が小さく、さらに演算回数も少なくて済むので、その分誤差が小さくなっているのだと思います。

おわりに

とりあえず実装はできました。が、kが小さい値でないと計算上誤差が大きすぎて使い物にならないプログラムになってしまいました。改善できたらまた記事に書きます。
気が向いたら秘密分散法でファイルを分散保存するプログラムとか自作してみたいと思います。